Quicksort: Cepat Kilat Urutkan Data dengan Rekursi

Oleh Samuel Wirajaya (website)

Co-founder, Acutis Academy. Software Engineer eks-FAANG, penggemar UNIX & Linux.

Gambar dua anak bermain dengan kartu-kartu bilangan

Beberapa waktu yang lalu kita sudah membahas tentang algoritma Insertion Sort yang bisa kita gunakan untuk mengurutkan data yang jumlahnya sedikit. Tapi bagaimana kalau setumpukan data kita ada ribuan atau jutaan banyaknya? Jika menggunakan insertion sort, pengurutan ini bisa saja memakan waktu yang terlalu lama. Maka dalam kesempatan ini kita akan membahas tentang algoritma pengurutan cepat atau quicksort.

Dengan algoritma ini, pengurutan dapat dilakukan secara cepat sekalipun kita menghadapi segunung data yang tidak beraturan.

Pengertian Quicksort

Algoritma quicksort adalah algoritma pengurutan yang memanfaatkan kekuatan rekursi dan teknik divide and conquer untuk mengurutkan sejumlah data tanpa memakan banyak waktu.

Apa itu Divide and Conquer?

Dalam pendidikan kewarganegaraan di Indonesia, kita mungkin sudah pernah mendengar versi bahasa Latin dari istilah ini, yaitu divide et impera. Ini adalah sebuah istilah yang menggambarkan betapa mudahnya para penjajah menaklukkan suatu bangsa yang terpecah belah.

Para ahli ilmu komputer pun mengambil inspirasi dari hal ini. Sebuah masalah dipecah-belah menjadi sub-masalah yang bisa dengan mudah diselesaikan, lalu menggabungkan solusi-solusi dari sub-masalah tersebut menjadi satu solusi untuk masalah yang semula. Maka dalam bidang algoritmika teknik “pecah-belah lalu taklukkan” ini mempunyai nama keren yang disebut divide and conquer.

Seringkali, sub-masalah dari sebuah masalah mempunyai struktur yang serupa dengan struktur masalah aslinya. Dalam hal ini, divide and conquer dapat menggunakan teknik rekursi.

Dalam rekursi, sub-masalah akan dipecah belah lagi menjadi “sub-sub-masalah” dan seterusnya, hingga tercapai kasus dasar yang bisa diselesaikan dengan sangat mudah. Dalam hal quicksort misalnya, ketika data yang harus diurutkan hanya satu butir saja, maka data tersebut sudah pasti terurut. Penyelesaian terhadap kasus dasar ini lalu digabungkan kembali untuk mendapatkan solusi terhadap masalah awalnya.

Langkah-langkah Quicksort

Untuk lebih jelaskan, kita perhatikan sketsa langkah-langkah quicksort sebagai berikut:

Pilih pivot: Dalam hal quicksort, pivot adalah sebutir data yang menjadi sebuah titik acuan untuk langkah berikutnya (yaitu, memilah data). Pivot ini bisa dipilih mana saja, misalnya adalah butir pertama dari data yang ada.
Pilah data menjadi dua kelompok: “kerdil” dan “raksasa”. Butir-butir data yang lebih kecil atau sama dengan pivot, kita sebut kerdil, dan butir-butir data yang lebih besar daripada pivot kita sebut raksasa.
Jalankan perintah quicksort(kerdil). Secara rekursif, kita terapkan quicksort pada kelompok kerdil, jadi kita dapatkan butir-butir yang termasuk dalam kelompok kerdil yang sudah terurut.
Jalankan perintah quicksort(raksasa). Secara rekursif juga, kita terapkan quicksort pada kelompok raksasa jadi kita dapatkan butir-butir dalam kelompok raksasa yang sudah terurut juga.
Susun hasil akhirnya sebagai berikut:

a. para kerdil yang sudah berurutan (dari langkah 3)

b. pivot

c. para raksasa yang sudah berurutan (dari langkah 4)

Kasus dasar dalam quicksort adalah jika data yang diurutkan hanya nol atau satu butir saja. Dalam kasus dasar ini, langkah-langkah di atas tidak perlu lagi dilakukan, karena data itu sudah pasti terurut.

Contoh Implementasi Kode Quicksort

Quicksort bisa diwujudkan secara sederhana dengan kode Python berikut:

def quicksort(arr):
    if len(arr) < 2: # kasus dasar
        return arr
    else:            # langkah rekursif
        pivot = arr[0]
        kerdil = [i for i in arr[1:] if i <= pivot]
        raksasa = [i for i in arr[1:] if i > pivot]
        return quicksort(kerdil) + [pivot] + quicksort(raksasa)

Atau dalam Snap!:

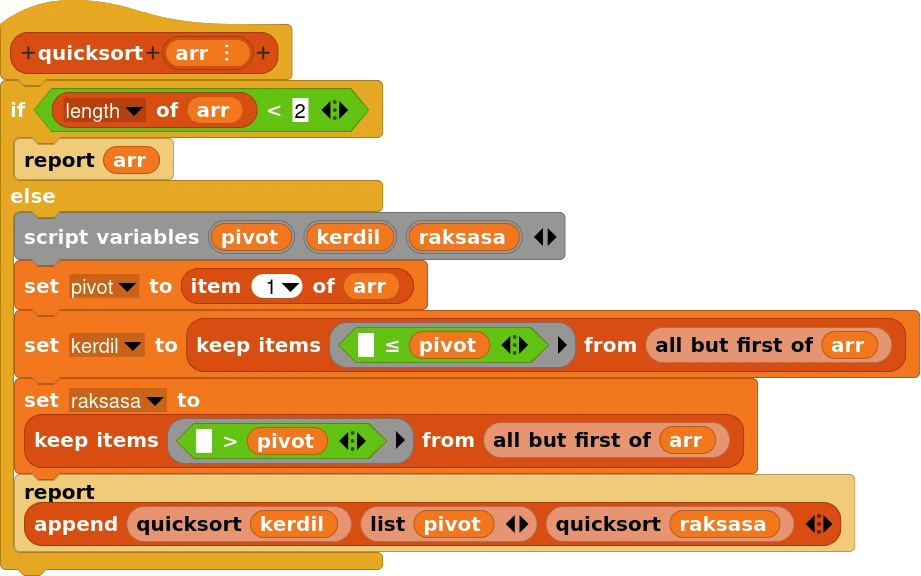
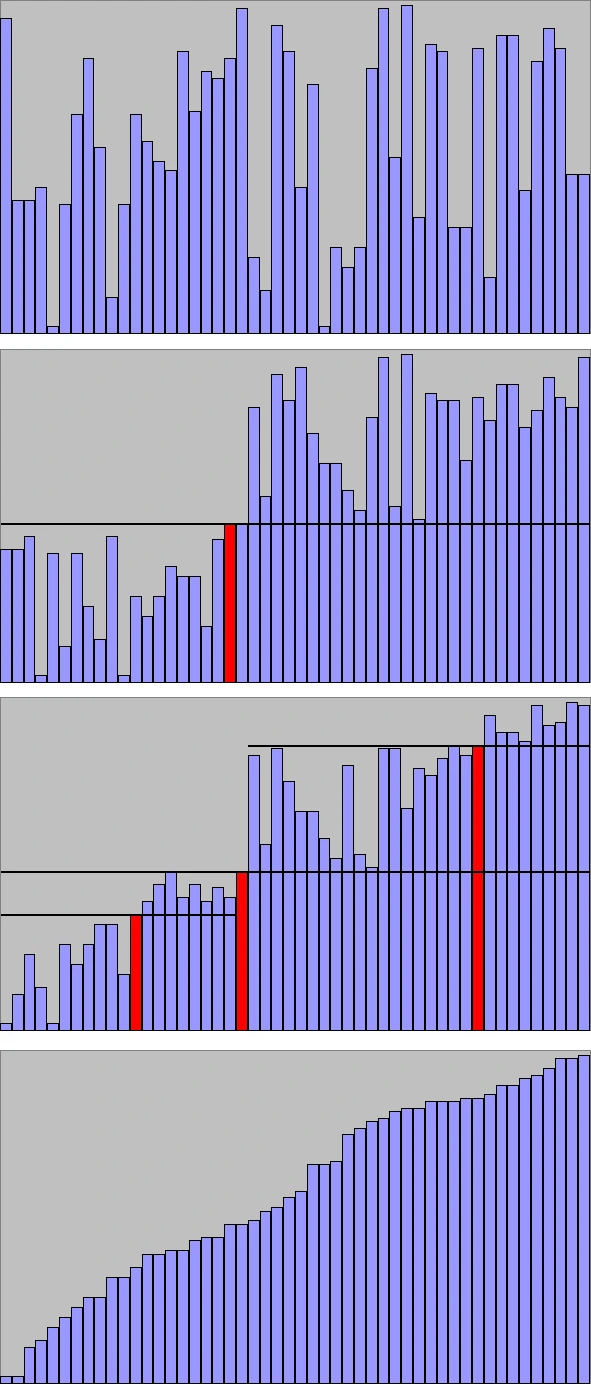
Berikut adalah gambar-gambar untuk membantu visualisasi langkah-langkah quicksort di atas. Pivot yang dipilih digambar dengan warna merah, dan kita bisa melihat bahwa setelah pivot dipilih, data akan dipilah yang lebih kecil dan lebih besar daripada pivot.

Visualisasi Quicksort — Gambar visualisasi quicksort. (Public domain: link sumber)

Keunggulan Quicksort

Keunggulan terbesar dari quicksort adalah keindahannya. Algoritma ini sangat mudah diingat, dan merupakan suatu contoh penerapan rekursi yang sangat berguna dalam dunia nyata.

Keunggulan lainnya dari quicksort adalah efisiensi, seperti yang dijanjikan oleh namanya. Jika kita melakukan analisis efisiensi, maka kita bisa buktikan bahwa performa waktu rata-ratanya adalah $O (n log n)$ . Dalam kata lain, algoritma pengurutan ini termasuk salah satu yang tercepat.

Selain itu, sebagai bentuk optimasi, algoritma quicksort dapat dibuat tanpa menggunakan memori tambahan yang besar (in-place quicksort) sehingga penggunaan memori bisa diminimalkan, dan performa bisa dimaksimalkan.

Untuk mengurangi overhead dan meningkatkan performa lebih lanjut lagi, kita juga bisa mengganti kasus dasar dalam kode program untuk memanggil Insertion Sort jika data yang diurutkan hanya sedikit (misalnya, kurang dari 15 butir.)

qsort, salah satu varian quicksort, menjadi sebuah fitur dalam bahasa pemrograman C dalam sistem operasi Unix pada tahun 1972, dan nama qsort melekat sampai hari ini dalam pustaka standar bahasa C (libc) walaupun algoritmanya berubah, karena beberapa kerugian yang dijelaskan di bawah ini.

Kerugian Quicksort

Walaupun quicksort adalah suatu algoritma yang bisa ditulis secara indah dengan metode rekursif, terdapat berbagai kelemahan yang perlu diperhatikan sebelum menggunakan quicksort dalam dunia nyata.

Performa dalam kasus terburuk

Kerugian dari quicksort adalah walaupun relatif cepat untuk data yang tersusun secara acak, terdapat kasus-kasus di mana quicksort menjadi lambat. Contohnya dalam kasus di mana data yang dimasukkan ternyata sudah berurutan.

Misalnya dalam implementasi quicksort yang dicontohkan di atas, jika kita memasukkan data yang sudah berurutan seperti 1, 2, 3, 4, 5, maka quicksort akan melakukan banyak sekali operasi perbandingan (sebanyak 8 + 6 + 4 + 2 = 20 kali), dan hasilnya adalah data yang sama 1, 2, 3, 4, 5.

Atau jika kita coba memasukkan data yang berurutan terbalik seperti 5, 4, 3, 2, 1, bisa diperhatikan bahwa gerakan masing-masing butir data akan mirip seperti insertion sort (hanya saja terbalik) dan operasi perbandingan yang dilakukan (20 kali) lebih banyak daripada jika kita menggunakan insertion sort (1 + 2 + 3 + 4 = 10 kali).

Beban overhead

Kelemahan di atas dapat diatasi dengan cara memilih pivot yang lebih baik, agar setiap kali data dipilah menjadi kelompok kerdil dan raksasa, maka banyaknya data di masing-masing kelompok adalah seimbang. Satu cara yang umum adalah memilih nilai tengah (median) dari elemen pertama, tengah, dan terakhir. Tetapi jelas bahwa pemilihan pivot seperti ini juga menambah overhead keseluruhan dari algoritma ini.

Selain itu, beban overhead dari algoritma ini juga berasal dari penggunaan teknik rekursi. Maka dari itu, jika data yang perlu diurutkan hanya sedikit saja, algoritma insertion sort mungkin akan lebih cocok.

Stabilitas Quicksort: Tidak Stabil

Dalam konteks algoritma pengurutan, stabilitas adalah bagaimana algoritma pengurutan itu menghadapi situasi di mana terdapat beberapa butir data yang sama atau sebanding. Jika sebuah algoritma pengurutan itu stabil, maka urutan elemen-elemen yang sebanding akan dipertahankan.

Tetapi implementasi quicksort seperti yang diuraikan di atas tidak demikian. Misalnya kita mempunyai data seperti ini:

2023-03-02  Happy Times Part 1
2023-03-02  Happy Times Part 2
2023-03-03  Music Festival
2023-03-03  Party Night
2023-03-04  Sports Day
2023-03-01  The Big Show
2023-03-01  The Celebration
2023-03-01  The Event Show
2023-03-01  The Gala
2023-03-02  The Party

Perhatikan bahwa judul-judul event di atas sudah berurutan secara alfabetik, namun tanggalnya masih perlu kita urutkan.

Jika kita menggunakan sebuah algoritma sort yang stabil, maka hasilnya akan menjadi seperti di bawah ini, yaitu tanggalnya terurut dengan baik dan urutan dari masing-masing butir akan dipertahankan seperti urutan aslinya:

2023-03-01  The Big Show
2023-03-01  The Celebration
2023-03-01  The Event Show
2023-03-01  The Gala
2023-03-02  Happy Times Part 1
2023-03-02  Happy Times Part 2
2023-03-02  The Party
2023-03-03  Music Festival
2023-03-03  Party Night
2023-03-04  Sports Day

Tetapi, jika kita menggunakan implementasi quicksort yang dicontohkan di atas, hasilnya akan menjadi:

2023-03-01  The Gala
2023-03-01  The Event Show
2023-03-01  The Celebration
2023-03-01  The Big Show
2023-03-02  The Party
2023-03-02  Happy Times Part 2
2023-03-02  Happy Times Part 1
2023-03-03  Party Night
2023-03-03  Music Festival
2023-03-04  Sports Day

Karena itulah, algoritma quicksort bisa kita sebut tidak stabil karena tidak mempertahankan urutan awalnya untuk elemen yang sebanding. Hal ini menyebabkan quicksort kurang cocok untuk pengurutan tabel.

Jika stabilitas pengurutan dikehendaki, maka kita bisa memilih algoritma sort yang stabil, misalnya merge sort, yang akan dibahas dalam kesempatan mendatang.

Kesimpulan

Algoritma quicksort memiliki kelebihan yaitu dapat mengurutkan data dengan cepat dan efisien, serta mudah diimplementasikan. Namun, algoritma ini juga memiliki kekurangan, seperti stabilitas yang tidak baik dan performa yang buruk dalam kasus-kasus tertentu.

Dalam prakteknya, quicksort dapat digunakan untuk mengurutkan data yang besar dan kompleks, tetapi perlu diingat bahwa algoritma ini tidak cocok untuk mengurutkan data yang kecil dan sederhana. Oleh karena itu, kita perlu memilih algoritma yang tepat untuk setiap kasus yang kita hadapi.

Dengan demikian, kita telah memahami konsep quicksort dan kelebihan serta kekurangan algoritma ini. Kita dapat menggunakan pengetahuan ini untuk mengurutkan data dengan lebih efektif dan efisien dalam prakteknya.